Update 17-Aug-2021. — The original algorithm discussed below has been enhanced and integrated in the IdExtenso framework. It now supports various range elision schemes, e.g. 42-5, 132-6, 210-11, 352-65, 1021-3... (Oxford style.) Additional features have been implemented, like the reciprocal routine, parse, which takes a raw range sequence and returns the associated array of numbers. Very useful for targetting and processing pages from the UI of your InDesign script.

New implementation: $$.PageRange module (IdExtenso), and sample script.

Sorting algorithms are extensively debated in the literature. In the JavaScript playground, however, I didn't find much about the particular case of sorting and formatting page numbers into smart and pretty ranges. As for the numerical sorting itself, benchmark results show that Array.sort(function(a,b){return a-b}) is almost always the fastest method, since Array.sort(…) is a built-in mechanism, very efficient—provided that the callback function itself is efficient!

The powerfulness of the native sort remains indisputable in ExtendScript as well. Anyway, some interesting refinements can be done in how we setup the process, based on the following observations:

1. myArray.sort() goes faster than myArray.sort(myCallback), meaning that if we can encode every relevant data as a simple String (i.e. UTF-16 stream or single value), then the sorting stage will be more efficient. Since an InDesign document cannot handle more than 9,999 pages, it can be reasonably assumed that any page number will remain in the range 1..0xFFFF, even in the event of eccentric numbering gaps.

Note: charArray.sort() is about 2X faster than intArray(function(a,b){return a-b}) in ExtendScript, testing on 500-length equivalent arrays. This topic is explored in more depth in a more recent article, “Reconsidering Array.sort() in ExtendScript/JavaScript”.

2. Scripts that deal with page numbers (searching, indexing, etc.) often involve text locations and, therefore, redundant page numbers. Thus, there is good chance for the input stream to contain sparse duplicates such as {10, 22, 10, 15, 10, 15, 22...}. By happy coincidence JavaScript easily handles lazy arrays based on sparse indices. Instead of sorting a sequence like [10, 22, 10, 15, 10, 15, 22], we can at no significant cost feed an intermediate array “by index”—a=[]; a[10]=xxx; a[22]=xxx; a[10]=xxx /*...*/—which somewhat removes the duplicates before further processing.

3. Then, using the index-based data structure described above, checking for holes or contiguous indices is dramatically simple. If a[i] is set (not undefined), then an incoming number i is already managed and does not require any operation. Otherwise, we can quickly inspect the state of both a[i-1] and a[i+1] to decide when and how to extend or merge existing ranges.

Lazy Multi-Range Array

I realized that all those preparatory steps can be carried out in a single pass with no sorting at all. So Array.sort() is delayed and finally applied to a reduced array of strings that only reflects the starting numbers of the ranges (with no duplicates). Once these starting numbers are ordered, we can traverse the data structure to format the output, with respect to some custom parameters.

Here is a picture of the data structure I am going to use:

The “Lazy Multi-Range Array” structure has good performance in JavaScript.

The key idea is that any range is entirely defined by its starting and ending values, and that we only want to manage the insertion of new values—which happen to be positive integers.

Any incoming value k can be instantly categorized as actually new—i.e. “not yet in the set”—iff a[k] is undefined. This condition allows us to skip duplicates and to focus on new elements. Now, suppose that at any given time the two following rules are satisfied:
• any singleton i is specified by the property a[i]==i;
• any range i..j is specified by the properties a[i]==j AND a[j]==i.

Note that those rules reflect in fact the same principle: a[i] points out to the ending point (j) while a[j] points out to the starting point (i). In the specific case of a singleton, we simply have i==j, so a[i]==i.

The reflexive relationship between indices and values at both ends of the interval has a remarkable consequence: no matter how the set evolves, we will never need to rewrite the values inside a range.

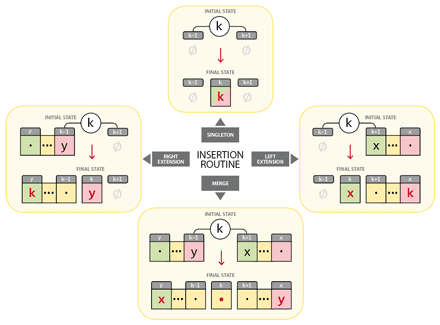
Indeed, any insertion will be done in O(1) by just checking the states at [k-1] and [k+1] so that we can instantly write and/or rewrite the pointers accordingly. The figure below illustrates the four possible cases:

Inserting a new value in the set.

The red values represent the writing operations. In the MERGE case—where k exactly fills the hole between y..(k-1) and (k+1)..x—identifying x and y requires no lookup since y==a[k-1] and x==a[k+1] :) Then the ranges are merged by just reassigning [x] and [y] in a reflexive way:
    a[x]=y and a[y]=x.
We also have to make sure that a[k] does not remain undefined, which is done by arbitrarily setting a[k] to k. (Provided that k is now inside a range, this value is of no importance as long as it is defined.)

The process we have exposed leads (almost instantly in JavaScript) to a pretty effective representation of any incoming stream of integers. Searching and sorting operations have been avoided at all. However, as we now have to traverse that structure in a consistent way to compute the final output, it would be astute to maintain a separate table of starting indices during the insertion steps (see the “Companion Array” in the first figure, above).

This is where we use the compact form of a String (UTF-16 values), each charcode representing the starting point of a range. This additional structure implies some crafts that complicate my implementation a bit, but I observed a significant performance gain with it, especially when processing large amounts of sparse ranges.

Implementation

In the end, this new strategy seems to go about 1.5X faster than the original one in various realistic conditions, and can be extremely faster in pathological conditions. (I found no serious example where it would be slower, but feel free to contradict me!)

function formatPgRanges(numbers,separator,joiner,minWidth,tolerance)
//----------------------------
// Formats an array of positive integers into an ordered sequence
// of single numbers and/or ranges. Returns the formatted string.
// ---
// NOTE: Rewritten version of our original formatRanges routine
// (cf. bit.ly/18cHfhB ). The present code *only supports positive
// integers in [1..65535]*, which should be sufficient since
// InDesign addresses at most 9999 pages.
// Improvements:
// * About 1.5X faster than the original routine (in avg cases)
// * Fix: [10,12,14]=>"10-14" when minWidth<=4 and tolerance==1
// ---
// <numbers>
//      Array of integers in [1..65535] [required]
//      The page numbers to format. Supports: empty
//      array, unsorted array, duplicated elems
// <separator>
//      String [opt] -- Default value: ", "
//      A string inserted between each result.
//      Ex.: formatRanges([4,1,3,8,9,6], " | ")
//          => "1 | 3-4 | 6 | 8-9"
// <joiner>
//      String [opt] -- Default value: "-"
//      A string used to format a range.
//      Ex.: formatRanges([4,1,3,8,9,6], ", ", "_")
//          => "1, 3_4, 6, 8_9"
// <minWidth>
//      Number [opt] -- Default value: 1
//      Minimum distance between the 1st and the
//      last number in a range.
//      Ex.: formatRanges([1,2,4,5,6,8,9,10,11], '', '', 1)
//          => "1-2, 4-6, 8-11"
//      Ex.: formatRanges([1,2,4,5,6,8,9,10,11], '', '', 2)
//          => "1, 2, 4-6, 8-11"
//      Ex.: formatRanges([1,2,4,5,6,8,9,10,11], '', '', 3)
//          => "1, 2, 4, 5, 6, 8-11"
// <tolerance>
//      Number [opt] -- Default value: 0
//      Number of allowed missing numbers in a range,
//      as suggested by Peter Kahrel (http://bit.ly/cABqIP)
//      Ex.: formatRanges([2,3,5,8,12,17,23], '', '', 1, 0)
//          => "2-3, 5, 8, 12, 17, 23"
//      Ex.: formatRanges([2,3,5,8,12,17,23], '', '', 1, 1)
//          => "2-5, 8, 12, 17, 23"
//      Ex.: formatRanges([2,3,5,8,12,17,23], '', '', 1, 2)
//          => "2-8, 12, 17, 23"
{
    // Defaults
    // ---
    separator||(separator=", ");
    joiner||(joiner="-");
    ( minWidth !== ~~minWidth || 1 > minWidth )&&(minWidth = 1);
    tolerance = ( tolerance !== ~~tolerance || 0 > tolerance )?
        0 : (1+tolerance);
 
    // Aliases
    // ---
    var chr = String.fromCharCode;
 
    // Init
    // ---
    var a = [],
        s = '',
        i = numbers.length,
        x, xMin, xMax, t,
        ret = '';
 
    while( i-- )
        {
        if( 0 >= (x=+numbers[i]) || a[x] ) continue;
 
        (xMin=a[-1+x])||(s+=chr(x));
        (xMax=a[ 1+x])&&(s=s.replace(chr(1+x),''));
 
        ( xMin&&xMax ) ?
            ( (a[x]=x),(a[xMin]=xMax),(a[xMax]=xMin) ) :
            ( (t=xMin||xMax)?((a[t]=x),(a[x]=t)):(a[x]=x) );
        }
 
    (t=s.length)&&(s=s.split('').sort().join(''));
 
    for(
        i=0, t--&&(xMin=s.charCodeAt(0))&&(xMax=a[xMin]) ;
        (i<t&&(x=s.charCodeAt(1+i)))||
        (i==t&&(x=Number.POSITIVE_INFINITY)) ;
        ++i&&(xMax=a[x])
        )
        {
        if( tolerance && (x-xMax <= tolerance) )
            { continue; }
        if( xMin + minWidth <= xMax )
            { ret += separator+xMin+joiner+xMax; xMin=x; continue; }
        for(; xMin <= xMax ;
            a[xMin] ? (ret += separator + xMin++) : ++xMin );
        xMin = x;
        }
 
    // Cleanup
    // ---
    (a.length=0)||(a=chr=null);
    return ret && (ret=ret.substr(separator.length));
}
 
 
// Sample code
// ---
var pages =      [13,33,10,20,100,12,15,33,35,33,11,99],
    separator =  " ; ",
    joiner =     "\u2013", // EN DASH (U+2013)
    minWidth =   2,
    tolerance =  1;
 
alert(formatPgRanges(pages, separator,joiner, minWidth,tolerance));
// => 10–15 ; 20 ; 33–35 ; 99 ; 100
 
 

Comments are always appreciated, by the way.